Note: A slightly different version of this article ran earlier on Gamasutra.com. I’ll be updating again later this week with a new article here so that you have something to read that hasn’t been previously published. Because I love you, man.
While I generally enjoyed Red Faction: Guerrilla, last year’s third-person action game from Volition and THQ, there was one type of mission on which I was lukewarm: The delivery missions where you were tasked with hopping in a vehicle and blundering over the Martian landscape to reach an arbitrary checkpoint before an equally arbitrary timer ran out. Meh. Pretty boring.
As a gameplay mechanic or goal, lots of games require you to complete challenges within a certain amount of time. Guitar Hero 5 and The Beatles: Rock Band have rewards for playing set lists within 1 hour and 1 day, respectively. And sometimes games inverse the formula and challenge you to keep the clock running by staying alive, such as in Left 4 Dead’s survival mode. But it’s generally the same goal: keep an eye on the timer and play the game, whether the specific task is mundane (driving across featureless plains or repetitive race tracks) or thrilling (fending hoards of zombies).
Turns out that recent research by Aaron Sackett at the University of Chicago and his colleagues 1 suggests a way that game designers could manipulate your perceptions of time to make these parts of the game more fun. In one study, the researchers had subjects listen to an annoying sound while they watched a timer tick the seconds off. For half the people, the timer was sped up by 20%; for others it was slowed down by 20%. Afterwords, subjects were asked the (frankly absurd) question of how enjoyable that all was. The result? Those whose clocks were sped up by 20% actually said the annoying sound was more enjoyable. Well, less terrible. Same thing.
But the phenomenon held true when people were doing something enjoyable to begin with. In a follow-up study, Sackett et al. had subjects listen to popular songs where the digital music player showed elapsed time for the track. In one group, the timer was sped up by 20% and in another it was slowed by the same amount. Again, people found this already pleasurable event even more enjoyable when they thought that time was passing more quickly and found it less enjoyable when time seemed to pass more slowly.
The researchers ran several more experiments, but the common theory explaining all their results was that when people experience unexpected distortions of time (i.e., time seemed to pass faster or slower than expected) they seek an explanation by turning to what psychologists call “metacognition,” or “thinking about thinking.” Specifically, Sackett hypothesizes that when faced with apparent time distortions people turned to the axiom that “time flies when you’re having fun” and concluded that because time flew (or dragged) they had fun (or didn’t). So much so that it affected how much fun they reported having and how likely they were to switch to other activities. He even did some additional studies where he manipulated the salience of this explanation in subjects’ minds and thus increased its effect. Time was affecting how much they enjoyed the game, not the other way around!
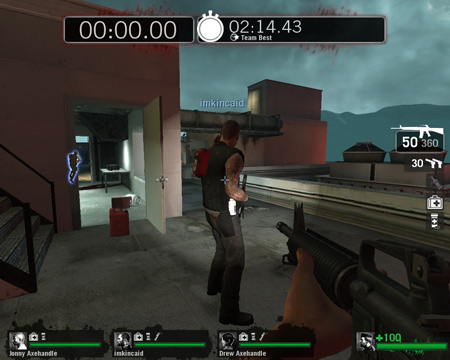
Congrats, team, you held off the zombie horde for ...TWO MONTHS AND FOURTEEN DAYS! Woo!
This has several interesting implications for game design. One devious thought that comes to mind deals with timed game demos. You could tell players that your demo will allow players to enjoy the game for 20 minutes before ending, then cut them off after 15 minutes. According to the above theory, people should think that those 5 minutes went missing on account of all the fun they were having.
But I can hear you the popping sound of your collective monocles now as you contemplate this base act of fibbing. 2. Fine, fine, other applications rely less on such crass deception. Take the driving missions in Red Faction: Guerrilla that I mentioned earlier. Speeding up the clock (after making adjustments to hold difficulty constant) should make that mundane task seem more enjoyable. Same for survival mode in Left 4 Dead or any other game that features a “fend off attackers for X minutes” mission. It would be interesting to see what would happen if you had the game say something like “Hold the enemies off for five minutes,” then NOT show a timer and then declare the challenge complete after just three minutes. If the research described above is to be believed, you should have more fun as long as you’re not aware of the time compression.
Sure, hardcore gamers armed with stopwatches and indignant outbursts will probably eventually figure it out, but I’ll bet a lot of them don’t and never hear about it from others. Heck, you can even add a little sweeping second hand if your User Interface Design person doesn’t have plans for the evening. If a little change in how the concept of time is presented makes for a noticeable change in how much players enjoy those bits of the game, it’s worth it. 3


Interesting research, particularly because it seems a subject doesn’t need to be consciously aware of what’s going on to engage in metacognition about the process.
Of course, I might argue that the solution to better FedEx missions lies more inCsikszentmihalyi – let’s actually make them engaging for the player! 😉
But the idea of manipulating a ‘timer’ of whatever sort to produce the desired effect is quite interesting. The trick is to be subtle enough so as to not alert the player that something fishy is going on.
When I talk about games being “fun” and someone replies, “But ‘fun’ is such a dubious term,” I say, “Well, actually, I use a relatively precise definition of ‘fun’: It’s measured by how long I can play without thinking about time.” I’m amused to see that my definition is supported by evidence. ^_^
Interesting thoughts, which touch on some well known concepts of time-shifting and awareness focus. I hold suspect though that simply changing an output device of a time measurement would get the effect. A player would have to both watch the timer and care about it for this to have any effect, which means the real lever to take advantage of this would be the addition of game play elements that focus the players attention on the task. And I agree that was completely missing from the Red Faction missions. A gradual build that played on the fear-of-loss psychology of humans would be far more effective.
@ Sean Dugan
True, let’s do both –make them more interesting and SEEM more interesting.
@ John Nesky
Fun is nebulous, but if someone tells me that they had fun (or didn’t) I tend to believe them.
@Christopher
Yeah, good point. The researchers made the subjects acutely aware of the timers.
huh,i thought time flies when you are having fun not the other way around,i never thought it can work the other way around.i have to test that somehow.
I think another important aspect would be how long people *think* they have been playing (asterisks added for emphasis). Say you are waiting for a particular monster to spawn in a given MMO, if you feel as though 5 minutes have passed when really 15 have, you probably are having more “fun” when compared to another person who feels like 30 minutes have passed when only 15 have. Just tossing out my two cents.
Nice article. Snappy. Cites nice research. Makes good connections.
I’ll only add these two observations to the mix.
In Super Mario Bros. the timer does not tick down in seconds. At a glance you may think you have “40” seconds left to reach the end, but it’s much less. Perhaps this is an early example that supports the research.
Likewise, in Street Fighter the match time ticks faster than seconds.